The mortal universe
In the current era of climate change and the global Covid-19 pandemic, it seems that urgent measures may be required to avoid catastrophic consequences. The speed with which the virus spreads and the influence of humankind on its own environment clearly demonstrates that we have become a global species, our feet now firmly planted in the Anthropocene. At the same time, when looked at from a broader perspective, we are in fact an insignificant form of life on astronomical scales, and are vulnerable to far more cataclysmic events than we are capable of producing ourselves. Perhaps contemplation and even solace can be found in this realization, but certainly such cataclysmic events are fascinating and not necessarily fatal.
There are very few things around us with a long lifetime – eventually time destroys all. Generally speaking, physical systems seek an optimal stable state. In the presence of external stimuli, this tendency is expressed in changes of state or so-called phase transitions. The paradigmatic phase transition is the formation of ice from water. If the cooling of water is rapid, the phase transition occurs in a continuous and undisturbed manner. Alternatively, it can happen that the gradual, undisturbed cooling of water results in supercooled water, which retains its liquid state, despite the fact that the formation of ice would be the more optimal energy outcome. Such a state is called a metastable state. In this example, due to a negligible deformation in the liquid, a bubble of ice is formed and quickly expands into the surrounding space. Such processes occur suddenly and the change of surroundings is rapid. In general, the phenomenon of metastability is extremely common and contributes to the durability of chemical substances in pharmaceuticals, for example. Another example of metastability is radioactivity where certain atoms have a limited lifespan, decomposing into more stable atoms by emitting light, electrons, and lighter nuclei, or by splitting into two nuclei. The larger the surface area of the phase transition, the more fascinating are the consequences – oceans may freeze over, entire Amazon rainforests erupt into flames. Over and above these examples, there exists the possibility of an almost unfathomable ultimate catastrophe where everything we know might disappear. It may be the case that our entire universe is suspended in a state of metastability. Thus, we can, with a vague sense of dread, attribute a limited lifespan to our own universe. To understand this remarkable concept, all we need is an elementary knowledge of the features of contemporary quantum physics.
A quantum catastrophe
In contrast to classical particles, it is impossible to simultaneously determine the position and velocity of quantum particles. As a consequence, quantum particles are harder to confine to a limited volume and are able to escape – in a process called quantum tunnelling – into areas that are "forbidden" to classical particles. In other words, quantum particles may travel through physical barriers in the same way that a ball might pass through the wall of a box without being harmed. What we call quantum fluctuations – minor changes in energy due to the imprecise position and velocity of a quantum particle – are responsible for the ability of the particles to tunnel through obstacles (shown on the picture below).
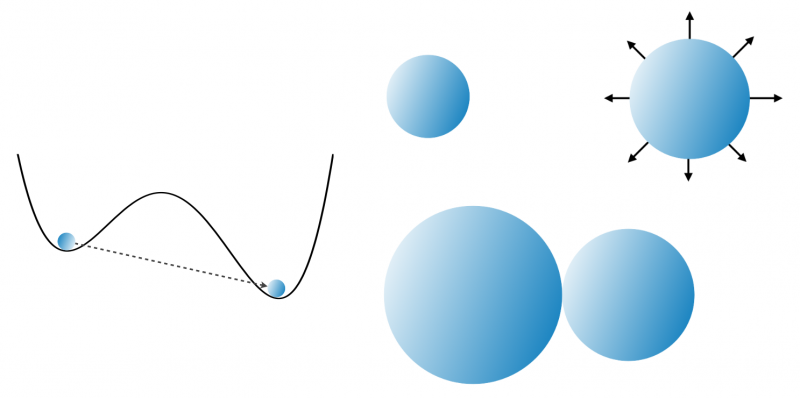
Relativistic quantum particles are described by quantum field theory in which physical fields extend throughout space-time. Light particles or photons are described by vector fields whereas electrons are described using different, so-called fermionic fields. We have known about this type of fields with internal direction for a long time. There are also scalar fields that have no directionality in space (the analogue in classical psychics would be temperature or pressure), but have a single attribute determined in space-time, a scalar value or a single number for each point in space-time. The particle corresponding to a scalar quantum field is the Higgs boson, which was discovered at the Large Hadron Collider (LHC) in 2012. Before that, the existence of scalar fields was merely a well-founded theoretical hypothesis. The discovery of the Higgs boson confirmed for the first time the existence of scalar fields as a reality. The crucial characteristic of the Higgs field is that it carries a constant value throughout the entire universe, a value that defines the energy minimum of the universe itself. This characteristic belongs exclusively to scalar fields because directional fields, such as vector and fermionic fields, cannot possess a constant directed value. This would contradict the principles of relativity.
We are now in a better position to understand the possibility of a quantum catastrophe. As in the case of supercooled water, the possibility exists that the constant value of the Higgs field is not in fact the absolute minimum. Instead, it may be that the field is stuck in a metastable state with an extremely long lifetime of at least 14.7 billion years (the higher valley on the left side of the above illustration). Just as water upon encountering impurities or thermal disturbances forms a bubble of ice that expands throughout the water, so too might a metastable scalar field tunnel into a more optimal energy state by way of quantum fluctuations (the lower valley on the left side of the above illustration). Should we live on the brink of ultimate cosmic collapse, quantum disturbances will nucleate a bubble somewhere in our universe within the characteristic decay time. Within this bubble, the Higgs scalar field would have a different value with a lower energy (the lower valley on the above illustration) than what was measured by the LHC collider.
Current measurements of the mass of the Higgs boson and other particles demonstrate that such a possibility indeed exists. However, there is a high probability that the lifetime of the universe is extremely long, approximately 10102–10241 years. This estimate, generated by a group from Harvard, holds within the Standard Model (SM) of fundamental particles, a minimal theory that accurately describes the great majority of measurable processes. Despite the great success of this theoretical framework, there are reasons to believe that SM does not provide a complete description of nature on the most fundamental level.
The most direct laboratory proof for this shortcoming of SM are the measurements of neutrino oscillations that would require massive neutrinos in contrast to the hypotheses of SM, which predict neutrinos with zero mass. Similarly, SM does not explain the existence of dark matter or provide a dynamic explanation for the fact that there is significantly more matter in the universe than anti-matter. Whatever the motivation may be to modify the SM, the energy properties of scalar fields would change in theories that extend beyond the SM. This means that with the addition of new fields, new minima (new valleys in the energy landscape) are created, or alternatively new ground states appear. In this example, our universe is either completely stable or it has a shorter lifespan than the SM predicts.
Polygonal advance
Determining the lifespan of a metastable vacuum in theories with multiple scalar fields is an interesting challenge in physics and a demanding problem to calculate. In recent years, the members of the Jožef Stefan Institute and the author of this paper, Miha Nemevšek, in collaboration with the doctoral student Victor Guada and our colleague Alessio Maiezza from the Ruđer Bošković Institute in Zagreb, developed a successful method to simplify the search for the decay time of metastable states. The idea is simple: instead of directly solving the equations that describe a metastable valley in the above illustration, we divide the path into linear sections. We know the solution for each individual segment and we can combine them into a smooth function that contains only one unknown variable. It turns out that the search for the final solution is much simpler and numerically stable than the solution to the original problem. When this kind of polygonal scaffolding is erected, we can add non-linear parts to it, and, with a little more effort, describe higher order corrections. Additional sections and non-linear corrections make it possible for us to generate a precise and rapid method that calculates the lifetime of the universe. The development and testing of robust polygonal methods is a relatively time-consuming process. For this reason we developed a handy program called FindBounce that many of our colleagues in the field now use. It is simple to use and can quickly deliver the relevant quantities that characterize phase transitions related to vacuum decay.
Hot bubbles
As was described in the introductory example, the sudden formation of bubbles in an empty space is triggered by quantum fluctuations. Understanding the environmental conditions in the early universe allows us to generate a qualitatively different physics background for similar processes. By measuring the frequency shifts in the spectra of stars, we know that galaxies are moving farther away from us, which proves that the universe is expanding. This means that in the past it was considerably smaller and hotter. The measurements of abundancies of light elements and dark matter show that in the past the universe was comprised of a hot gas, made up of fundamental particles and light. This picture has an important impact on how we view the energy state of scalar fields in the early universe. Remarkably, at high temperatures, a stable energy minimum may become metastable. Rather than quantum disturbances, in these conditions it is the thermal fluctuations that would trigger the formation of bubbles with more optimal vacuum energy. The subsequent expansion of bubbles in the early universe includes interactions of the bubble wall with the gas of fundamental particles on each side of the wall, which computationally exacerbates the problem of understanding the phase transition, and therefore requires a more delicate analytical treatment.
Are we made of stardust or vacuum stuff?
In contrast to a catastrophe that would be caused by vacuum decay in an empty space, transitions that may have taken place during the early universe provide somewhat more optimistic possibilities. Perhaps the most promising aspect is the possibility of understanding the origin of our own existence. One of the riddles that the SM does not solve is the observed dominance of matter over antimatter. If the SM were correct, then equal quantities of matter and antimatter were formed in the early universe and would have annihilated each other. Only hot photon gas would have remained and a negligible quantity of matter, but this does not correspond to what we know about the early universe. How can the hypothesis about the formation of bubbles in the early universe explain this situation? The hypothetical mechanism relies on the movement of the newly formed bubble through a hot plasma (the gas of fundamental particles). The wall of the bubble divides two physically and fundamentally different worlds. On the outside of the bubble are particles that are still unknown to us and that have unknown interactions. If the properties of these new particles and the force between them is exactly right, then the membrane of the bubble will allow entry to more particles than antiparticles. In this way, our universe would be created inside of the bubble, formed by the plasma of known particles and light. As a result of the expansion of the bubble and subsequent space-time, the plasma would cool and create galaxies, stars, and planets in which matter dominates over antimatter.
In the framework of the SM it is not possible to create such Higgs field bubbles in the early universe at the high temperatures, a fact which was established by measurements taken at the LHC particle collider. In order for a bubble to form, the mass of the Higgs boson must be considerably smaller than the measured one. As already mentioned, there are reasons for extending the SM and many of the more complete models allow for the existence of phase transitions at high temperatures. A precise calculation of the formation of the dominance of matter over antimatter is quite demanding and contains various approximations. What can be determined with considerable precision is the probability of the formation of a bubble in the early universe, and we can also determine the temperature of the early universe when this probability was very high (it is called nucleation temperature). This problem is very similar to vacuum decay in an empty space and we can tackle it with the previously mentioned newly-developed polygonal method.
The sound of space-time
It is possible to test at colliders many models that might explain the dominance of matter over antimatter. The new particles may be entirely accessible to current searches at the LHC, where we are looking for particles with precisely the kind of properties that allow for cosmological transitions in the early universe. Given that we still have many years of work and data collection from the LHC collider, many researchers are working on this kind of research. There is another and much more quiet way to discover whether bubbles occurred in the early universe: namely, using the LIGO or Laser Interferometer Gravitational Wave Observatory that looks for gravitational waves, which are hardly discernible oscillations of space-time. In the LHC, we accelerate beams of protons to the highest energy levels achievable in a laboratory. With each collision, an explosion occurs and the particles are caught and measured by various detectors. In contrast to the cacophony of data that is filtered by the LHC, measurements of gravitational waves take place in exceptional silence. LIGO is comprised of two detectors on different sides of the U.S. Each interferometer has two four-kilometre-long arms along which a laser light beam travels, reflecting back and forth hundreds of times during its voyage. The task of the interferometer is to measure the gravitational waves as they make almost indiscernible changes to the length of the arms as well as the time it takes for the light to travel through the arms. These changes are extremely small. The smallest change in distance that the LIGO can measure is an incredible 10-19 m, which is one billionth of the size of a hydrogen atom.
One of the reasons that it took so many decades to directly measure gravitational waves was due to uncertainty about the number of sufficiently powerful sources of gravitational waves in the universe. Although we knew from the cooling of pulsars (neutron stars that emit beams of electromagnetic radiation) that these waves existed, not enough was known about the number of neutron stars and black holes, mergers of which are the primary source of gravitational waves. In the last four years, LIGO has successfully measured more than ten measurable events that are equivalent to the mergers of black holes with masses approximately ten times greater than that of the sun. If these events are not too far from the earth, we can determine, with the help of a third, less powerful observatory, the VIRGO observatory in Italy, the position of such events in the sky.
In addition to the mergers of black holes and neutron stars, the gravitational wave observatories are able to measure signals from phase transitions in the early universe. Throughout the entire space of the early universe, bubbles began to form when the universe cooled down to the nucleation temperature. These bubbles eventually collided and merged, leaving behind a turbulent stream of plasma made of particles and light (as shown on the upper righthand illustration). Using analytical estimates and numerical simulations, it is possible to determine the origin of these sources, and to predict the frequency and intensity of the collective signals of gravitational waves. In contrast to the localized mergers of black holes, collisions of bubbles in the early universe would trigger an even hum, similar to cosmic microwave background photons.
In the coming years, we expect colliders and gravitational wave observatories to become even more powerful and sophisticated. Thus, we will be able to conduct experiments with sensitivities at a much broader range of frequencies and with smaller intensities. It will be an interesting period for fundamental particle physics, a period when we will be able to ascertain which theoretical frameworks can be tested, and will also begin to have more control over the uncertainties in our models. Of course, the discovery of new signals would be incredibly exciting. It would open the door to new interactions, the understanding of neutrino masses, dark matter and – finally – our own existence.
Translated by Erica J. Debeljak















