Pojmovanje in razumevanje števil se je skozi čas spreminjalo in širilo v skladu s potrebami človeštva. Danes poznamo števila, ki opisujejo ne le količine in mere, temveč tudi gibanje, rotacijo in simetrijo v večdimenzionalnih prostorih. Med njimi imajo posebno mesto kvaternioni, ki jih bomo podrobneje predstavili.
Števila spremljajo človeka od pradavnine, ko se je naučil šteti. Skupaj z razvojem njegovih dejavnosti se je spreminjala tudi potreba po različnih vrstah števil, s katerimi je računal. Tako je potreba po odštevanju vodila k uvedbi negativnih števil, ki so se prvič pojavila v starih kulturah – na Kitajskem že okoli leta 200 pr. n. š., ko so pozitivna števila zapisovali z rdečo barvo, negativna pa s črno. Računske operacije med števili, kot jih poznamo danes, je uvedel Brahmagupta (598–668 n. š.), in sicer v Indiji, kjer so v 7. stoletju že poznali mestni zapis števil. Podobno je potreba po deljenju pripeljala do ulomkov. Znano je, da je Pitagora verjel, da se vse na svetu da izraziti s celoštevilskimi razmerji. Zgodba pravi, da je član njegove šole Hipaz, ki je dokazal, da √2 – v nasprotju s Pitagorovim prepričanjem – ni racionalno število, to ugotovitev plačal z življenjem. Množica realnih števil je bila natančno definirana šele v 19. stoletju. Matematiki so pokazali, da realna števila ne vsebujejo le algebrskih števil (npr. √2, ki je ničla polinoma x2 − 2 = 0), temveč tudi transcendentna števila, kot sta π in e, ki nista ničli nobenega polinoma s celimi koeficienti. Dva tisoč let kasneje je študij balistike vodil Niccolòja Tartaglio (1499/1500–1557) do enačb, ki so vsebovale korene negativnih števil. Tako je nastalo prvo imaginarno število, imaginarna enota , ki je rešitev enačbe. Dodajmo še, da je koren negativnega števila najbrž prvi zapisal Heron iz Aleksandrije (10–70 n. š.).
Števila, ki imajo obliko z = x + iy, kjer sta x in y realni števili, imenujemo kompleksna števila. Ta so realno dvorazsežna in jih predstavljamo v ravnini. Množico kompleksnih števil označujemo s C (oziroma s Ci , če želimo poudariti imaginarno enoto i), njeno ravninsko predstavitev pa imenujemo kompleksna ravnina. Ena zanimivejših formul, ki povezuje imaginarna, transcendentna in cela števila, je eiπ = –1.
Vsako kompleksno število lahko predstavimo v ravnini: število z = x + iy identificiramo z vektorjem (x, y). Kompleksna števila seštevamo po komponentah, kot bi seštevali ustrezne vektorje, med seboj pa jih množimo kot dvočlenike. Posebno vlogo pri tem imajo kompleksna števila, ki so velika 1. Po Pitagorovem izreku so to števila, za katera velja lzl = √x2 + y2 = 1. Množenje s takim kompleksnim številom ima geometrijski pomen: če je φ kot, ki ga vektor (x, y) oklepa s pozitivnim delom osi x , potem pomeni množenje s kompleksnim številom rotacijo za kot φ v ravnini, če kompleksna števila predstavimo z vektorji.
Zgoraj omenjena tesna povezava med ravninsko geometrijo in kompleksnimi števili je odprla naslednji problem: ali obstaja večja množica števil, hiperkompleksna števila, s katerimi bi bilo mogoče popisati ne ravninsko, temveč prostorsko geometrijo? »Oreh je bil trd, a se je nazadnje le vdal,« pravi v svoji knjigi Nihalo, prostor in delci slovenski matematik in univerzitetni profesor France Križanič. Novo množico realno 4-razsežnih števil je uvedel sir William Rowan Hamilton (1805–1865); poimenoval jih je kvaternioni. Ta števila so sestavljena na podoben način kot kompleksna števila, le da imajo namesto ene kar tri osnovne imaginarne enote (i, j, k), torej števila, za katera velja i2 = j2 = k2 = 1. Kvaternioni, ki jih Hamiltonu v spomin označujemo s H, so torej množica vseh števil oblike q = a + bi + cj + dk, kjer so a, b, c in d realna števila. V nasprotju s kompleksnimi števili, kjer je njihov produkt ponovno kompleksno število, pa pri kvaternionih ni povsem očitno, kako je treba definirati medsebojne produkte imaginarnih enot, da bo rezultat spet kvaternion. Če namreč dva kvaterniona kot štiričlenika množimo med seboj, dobimo naslednje produkte imaginarnih enot: ij, ji, ik, ki, jk in kj. Ko se je sir William v ponedeljek, 16. oktobra 1843, na poti do Kraljeve irske akademije z ženo sprehajal vzdolž Kraljevega prekopa v Dublinu, so se koncepti postavili na pravo mesto in posvetilo se mu je, da je formula, ki jo išče, tale: i2 = j2 = k2 = ijk = –1. V navalu navdušenja je formulo z nožičem vrezal v kamen na Broughamskem mostu. Danes je tam spominska plošča, 16. oktober 1843 pa velja za rojstni dan kvaternionov. Če formulo preoblikujemo, lahko izračunamo, da je ij = –ji = k, ik = –ki = –j, jk = –kj = i. Takoj opazimo, da produkt ij ni enak produktu ji, temveč mu je nasproten: ij = –ji. Pri množenju v množici kvaternionov torej ni vseeno, v kakšnem vrstnem redu sta faktorja, zato pravimo, da produkt v množici kvaternionov ni komutativen. Posebno pomembna je množica vseh kvaternionov, ki rešijo enačbo (a + bi + cj + dk)2 = –1. Krajši račun pokaže, da so rešitve enačbe dane s pogojema a = 0 in b2 + c2 + d2 = 1. Gre torej za čisto imaginarne kvaternione, ki so veliki 1, zato jih imenujemo imaginarne enote. Če konstrukcijo analogno nadaljujemo, lahko iz kvaternionov naredimo oktonione (realno 8-razsežna števila), iz teh sedenione (realno 16-razsežna števila) in tako naprej v neskončnost.
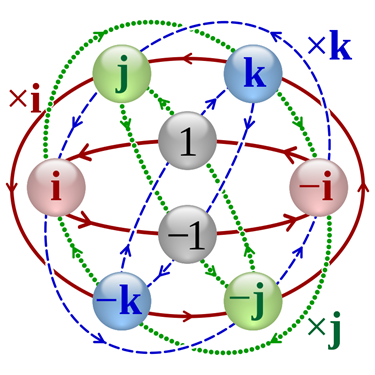
Slika 1: Hamiltonovo množenje, predstavljeno z grafom. Vir: Wikimedia Commons
V matematiki je že tako, da vsak na novo uvedeni formalizem sčasoma zaživi svoje življenje in s svojim razvojem prispeva tudi k drugim znanstvenim vejam. Po koncu 19. stoletja je zanimanje za kvaternione ugasnilo, raziskovalci pa so se usmerili k splošnejšim hiperkompleksnim številom in k drugim, z njimi povezanim algebrskim strukturam. V zadnjem času pa so kvaternioni spet postali bolj aktualni. Poleg uporabe v fiziki, kjer se da z njimi npr. opisati elektronski spin, se kvaternione danes uporablja tudi v numerični matematiki, in sicer pri iskanju poti v prostoru, ki imajo predpisane lastnosti. Nepogrešljivi so pri opisovanju gibanja togih teles, zlasti pri konstrukciji gibanja brez »nepotrebnih rotacij«, natančneje pri iskanju polinomskih krivulj, ki dopuščajo minimalno rotirajoče ogrodje (Farouki idr. 2017). V prostorski kinematiki se z uporabo kvaternionov pri opisovanju gibanja izognemo izgubi prostostnih stopenj, ki nastane pri določeni medsebojni legi rotacijskih osi (angl. gimbal lock), zato se jih uporablja v računalniški grafiki, računalniškem vidu, robotiki itd.
Geometri pa se niso ustavili le pri ravnini in prostoru, temveč so želeli koncepte s teh prostorov prenesti tudi na ploskve. Eden takih konceptov je pravokotni koordinatni sistem v ravnini (R2), prostoru (R3) in večdimenzionalnih prostorih (Rn). Vsem je dobro poznan tudi koordinatni sistem na sferi (poldnevniki in vzporedniki), ki je tudi pravokotni koordinatni sistem (razen v polih) – v (dovolj majhni) okolici vsake točke je namreč videti kot običajen koordinatni sistem v ravnini, kar s pridom uporabljamo v kartografiji. Geometri pa so zahtevali še več, namreč da bi lahko del ravnine preslikali na ploskev tako, da bi se ohranili vsi koti skupaj z orientacijo. Preslikavam s temi lastnostmi pravimo konformne. Poseben primer so konformne preslikave, ki iz podmnožic kompleksne ravnine slikajo kompleksno ravnino: imenujemo jih holomorfne. Takih funkcij je zelo veliko; skupaj s svojimi večrazsežnimi različicami so temelj kompleksne analize, ki je veja matematične analize. Matematiki 19. in 20. stoletja so pokazali, da ima vsaka točka na dani ploskvi okolico, ki je slika kroga v ravnini s preslikavo, ki ohranja kote. Koordinate, ki jih s tem dobimo na ploskvi, imenujemo izotermne koordinate.
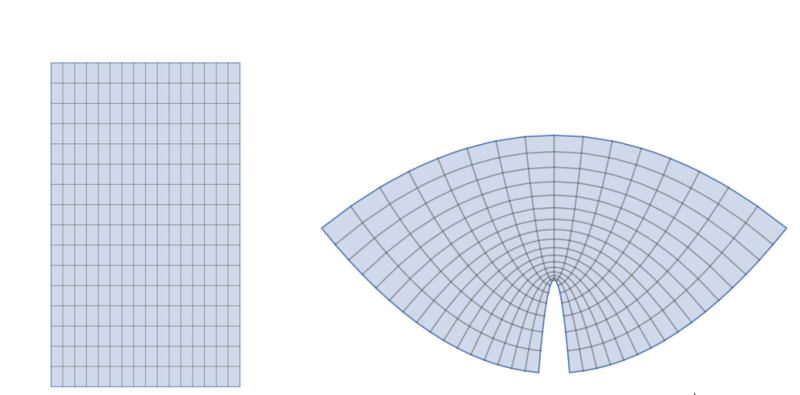
Slika 2: Pravokotnik in njegova konformna slika s prikazanimi izotermnimi koordinatami
Kako pa je z analognim problemom v višjih dimenzijah? Tu se srečujemo s posplošitvami pojma ploskve na objekte, ki si jih lahko predstavljamo kot večrazsežne ploskve; pravimo jim mnogoterosti. Izkaže se, da v večini večdimenzionalnih primerov izotermnih koordinat ne moremo vpeljati. V višjih dimenzijah je – v nasprotju s kompleksno ravnino – preslikav, ki ohranjajo kote, zelo malo. Že v trirazsežnem prostoru (R3) imamo na voljo samo premike, podobnost, ortogonalne transformacije in inverzije ter njihove kombinacije. Posledično je tudi družina kvaternionskih preslikav, ki ohranjajo kote, majhna, saj je prostor kvaternionov štiridimenzionalen. Zato je tudi kvaternionskih mnogoterosti, ki so lokalno konformne H, malo.
S soavtorjema Grazianom Gentilijem z Univerze v Firencah in Fabiem Vlaccijem z Univerze v Trstu se s področjem kvaternionov ukvarjamo že dalj časa. Zanimalo nas je ne samo to, kako lahko na to področje posplošimo pojme iz klasične kompleksne analize, temveč tudi, katere so tiste posebne lastnosti, ki so opazne le pri kvaternionih. V članku smo s pomočjo kvaternionov in kvaternionskih preslikav predlagali alternativno definicijo kvaternionskih mnogoterosti. Prostor kvaternionov vsebuje veliko kompleksnih ravnin, ki jih imenujemo rezine; vsaka imaginarna enota I določa svojo ravnino CI. Vsaka rezina določa svoj pravokotni komplement, to je ravnino, katere vektorji so pravokotni na vse vektorje rezine. Definirali smo, da so rezinsko konformne ali rezinsko izotermne preslikave v prostore Rn (za n vsaj 4) take, da njihove zožitve na rezine ohranjajo kote, prav tako pa ohranjajo kote tudi zožitve na pravokotne komplemente rezin. Dokazali smo, da je družina takih preslikav zelo velika in da se jih da konstruirati iz preslikav, definiranih na kompleksni ravnini. Predlagani pristop odpira novo poglavje v raziskavah konformnih struktur – raziskave rezinsko konformnih struktur. V članku smo pokazali še, da se da podobno definirati tudi rezinsko konformne strukture za oktonione. Naše nadaljnje raziskave kažejo, da obstaja med kompleksnimi strukturami in rezinsko konformnimi strukturami tesnejša povezava, kot smo prvotno pričakovali.
Upamo, da smo bralce prepričali, da kvaternioni niso le matematični konstrukt, ki našo predstavo o številih širi v štiridimenzionalni prostor, temveč da njihove posebnosti vodijo v novo geometrijo pa tudi v simetrije, ki so matematično izjemno bogate. Članek predstavlja razširitev konceptov iz klasične kompleksne analize na kvaternione, kar odpira vrata novim načinom razumevanja geometrije. Kvaternioni torej niso le zanimivost iz zgodovine matematičnih struktur, ampak živa veja sodobne matematike, ki nam pomaga razumeti svet na načine, ki si jih včasih ne znamo niti predstavljati.